Learn And Invert A Binary Search Tree In JavaScript

One of the most popular questions asked to software developers in an interview is "How do you invert a Binary Search Tree?".

The truth is that many of us do not even know what a Binary Search Tree is, let alone inverting it.

So let's start with the basics.

What Is A Tree?

A Tree is a widely-used data structure consisting of nodes connected by edges:

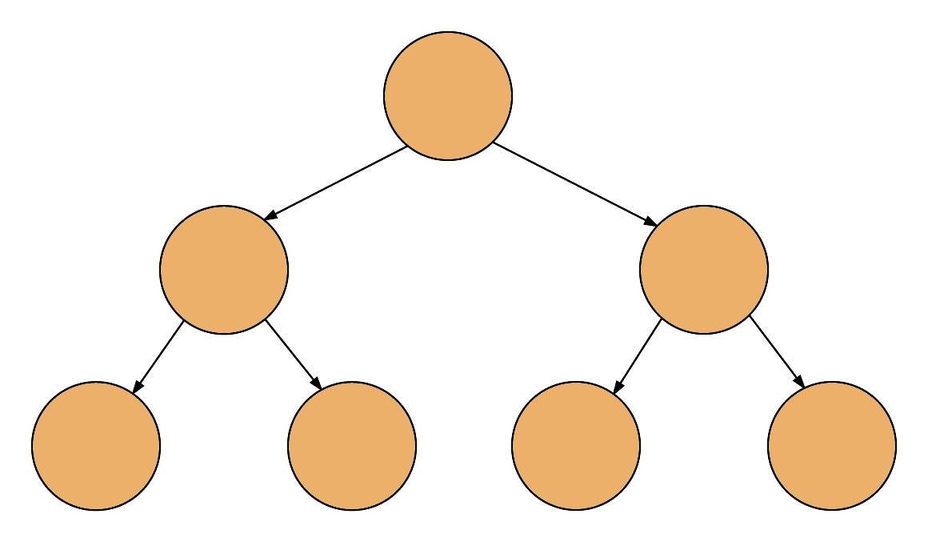
It is merely a collection of nodes, where each node is a data structure containing a value and references to its child nodes, with the restriction that there are no duplicate references and no reference to the root.

Terminology

To understand trees better, it is necessary to know at least the basic concepts.

Node - a structure containing a value and pointers to the child nodes.

Root Node - top node of the tree.

Internal Node - any node of the tree that contains at least one child node.

External/Leaf Node - any node of the tree that does not contain a child node.

Height of a Node - a length of the longest downward path from that node to a leaf node.

Depth of a Node - a length of the path to its root node.

Height of a Tree - a length from the root node to the deepest node in the tree.

Size of a Tree - a number of all nodes.

To learn more, read Wikipedia.

Tree Implementation In JavaScript

The implementation of a simple tree in JavaScript is straightforward:

class Node {
  constructor(value) {
    this.value = value;
    this.children = [];
  }
  
  addChild(node) {
    this.children.push(node);
  }
}

const root = new Node("root");
const child1 = new Node("child1");
const child2 = new Node("child2");
const child3 = new Node("child2");

root.addChild(child1);
root.addChild(child2);
child1.addChild(child3);

// Node {
//  value: "root",
//  children: [
//    Node {
//      value: "child1",
//      children: [ Node { value: "child2", children: [] } ]
//   },
//    Node { value: "child2", children: [] }
//  ]
// }
console.log(root);

What Is A Binary Tree?

Since we know the basics of a tree, let's take a look at a Binary Tree which is a specialized version of a tree.

In a Binary Tree, each node has at most two children, which are called left and right child.

Depending on the arrangement of the nodes, there are different types of Binary Trees:

• Full - each node has either 0 or 2 children (1 is not allowed)

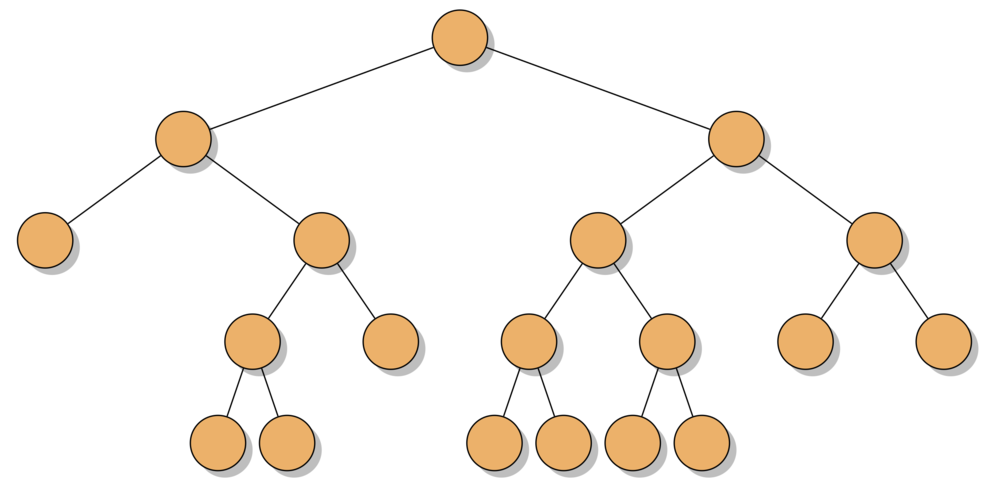
• Complete - every level, except possibly the last one, is full of nodes, and all nodes in the last level are left as far as possible

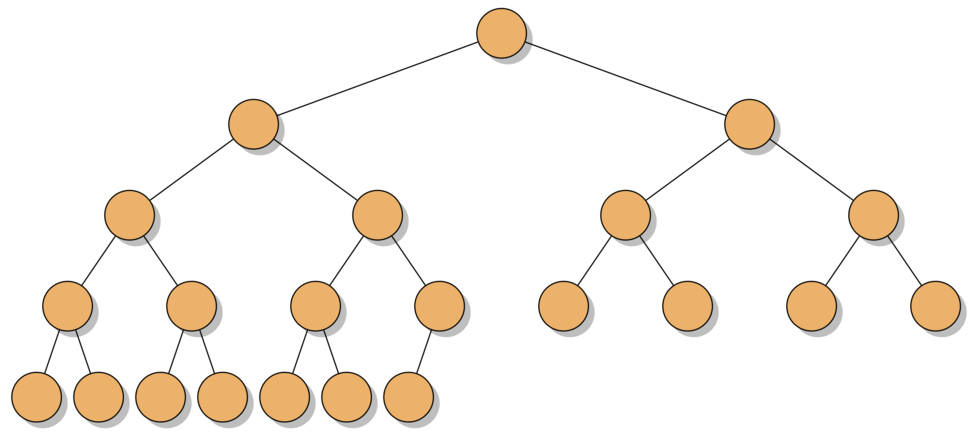
• Perfect - every level is full of nodes and all leaves have the same depth

What Is A Binary Search Tree?

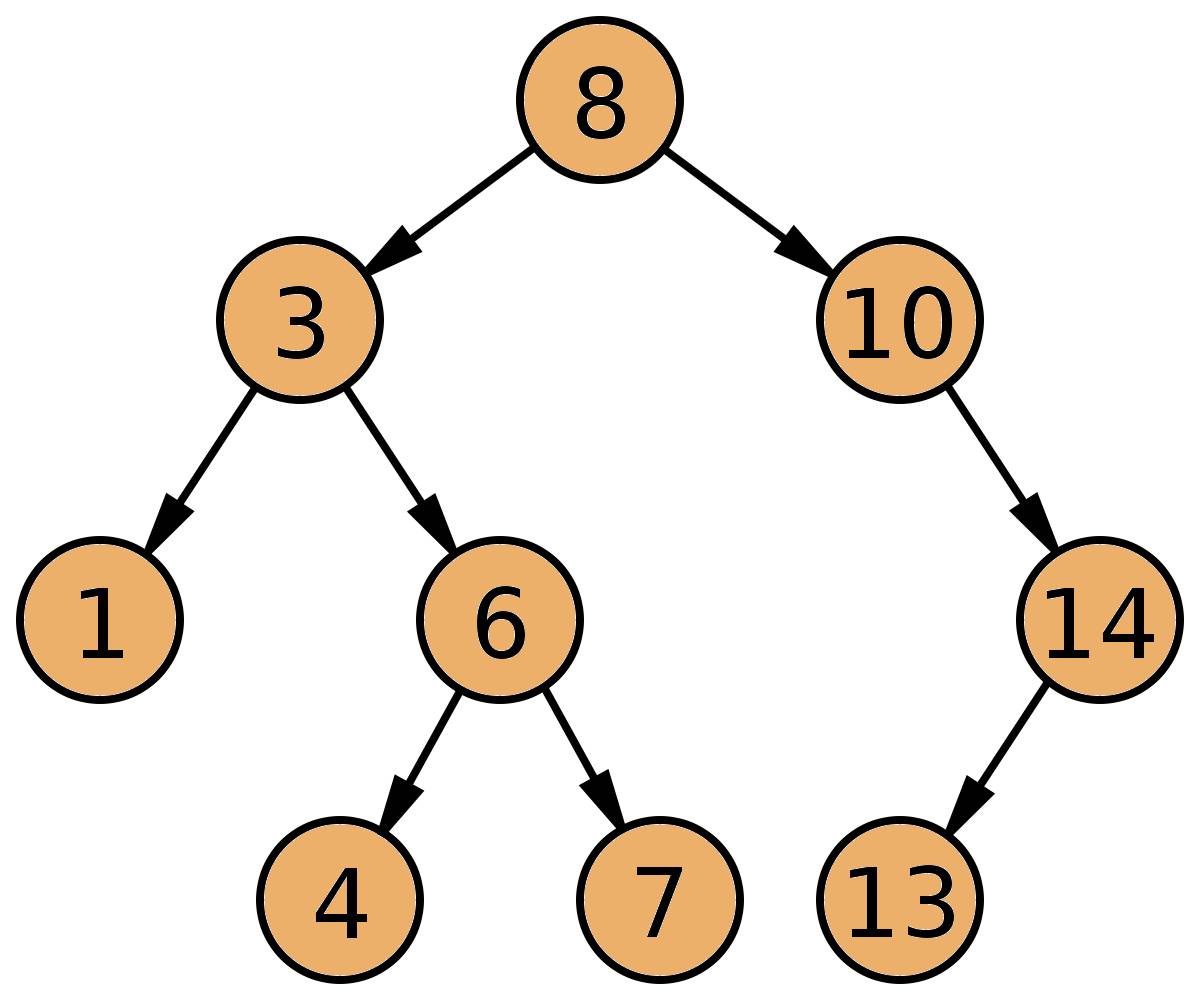
A Binary Search Tree is a special type of Binary Tree that contains a maximum of 2 nodes (like all Binary Trees) with one big difference - the values are set so that the left children must be smaller than the parent, the right children - larger:

Binary Search Tree Implementation In JavaScript

The basic implementation of Binary Search Tree in JavaScript (allows you to create a tree and insert nodes):

class Node { 
  constructor(data) {
    this.data = data; 
    this.left = null; 
    this.right = null; 
  } 
}

class BinarySearchTree { 
  constructor() { 
    this.root = null; 
  }
  
  insert(data) {
    const node = new Node(data);
    
    if(this.root === null) {
      this.root = node;
    } else {
      // Find the correct position
      // And insert the node
      this.insertNode(this.root, node);
    }
  }
  
  insertNode(rootNode, newNode) {
    // If the data is smaller than the root
    // Move to the left
    if(newNode.data < rootNode.data) {
      // If left is null
      // Insert here
      if(rootNode.left === null) {
        rootNode.left = newNode;
      // If left is not null
      // Recur untill null if found
      } else {
        this.insertNode(rootNode.left, newNode);
      }
    // If the data is greater than the root
    // Move to the right
    } else {
      if(rootNode.right === null) {
        rootNode.right = newNode;
      } else {
        this.insertNode(rootNode.right, newNode);
      }
    }
  }
}

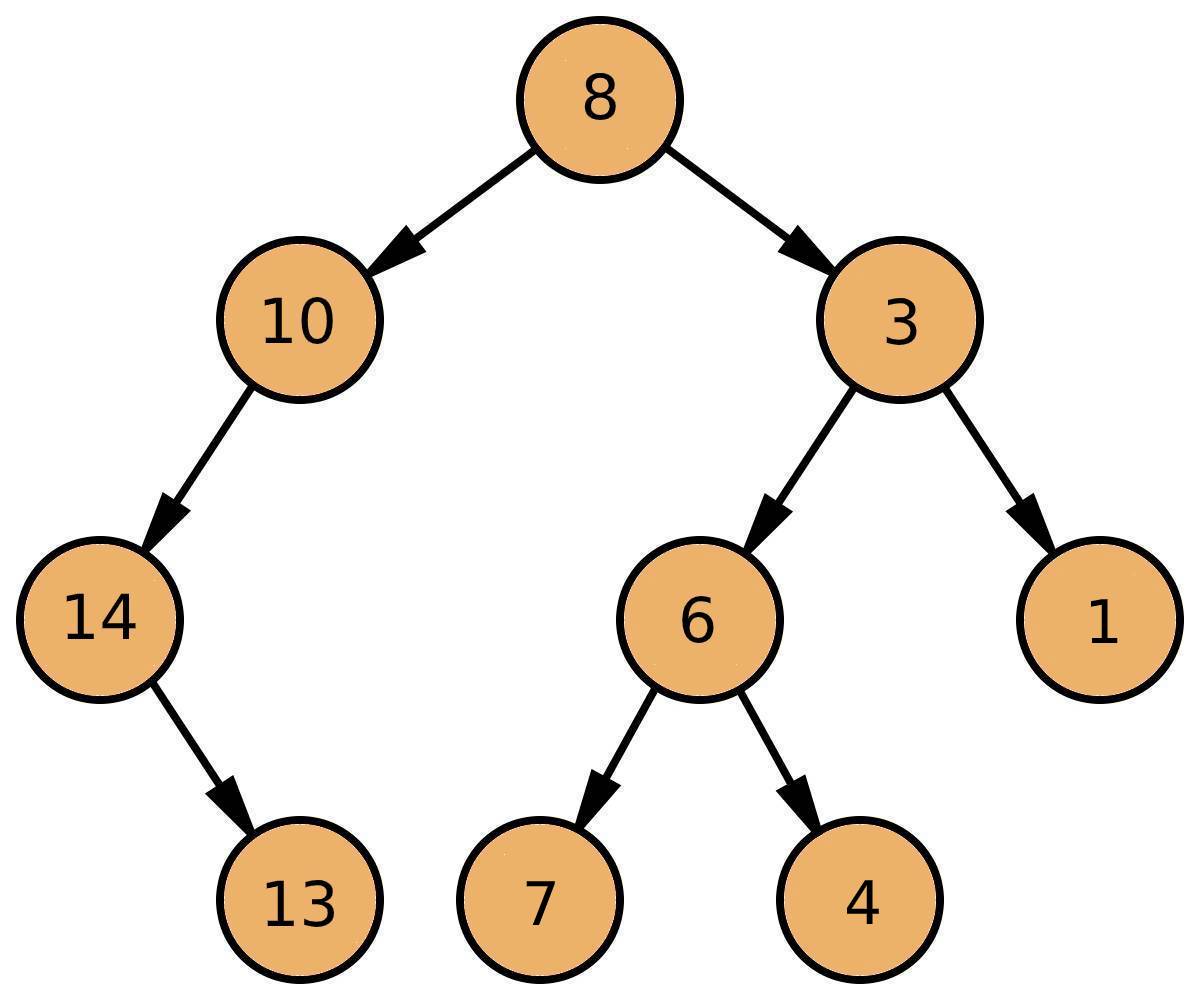
Create the same tree as in the example above:

const binarySearchTree = new BinarySearchTree();

binarySearchTree.insert(8);
binarySearchTree.insert(3);
binarySearchTree.insert(10);
binarySearchTree.insert(14);
binarySearchTree.insert(6);
binarySearchTree.insert(1);
binarySearchTree.insert(4);
binarySearchTree.insert(7);
binarySearchTree.insert(13);

Invert A Binary Search Tree

Now that one has the first knowledge of the given topic, it is finally possible to continue with the inversion of a Binary Search Tree.

But first of all: What does it mean to reverse a Binary Search Tree?

Basically, it means swapping left and right children:

const invertTree = (tree) => {
  if(!tree) {
    return;
  }
  
  const left = invertTree(tree.left);
  const right = invertTree(tree.right);
  
  tree.left = right;
  tree.right = left;
  
  return tree;
}

Inverted tree created in the example above:

Summary

Inverting a Binary Search Tree is not the number one skill you need these days, but it will definitely improve your general knowledge.

It is also asked quite often in interviews, so make sure you understand the topic and implement the inverting algorithm at least once from memory.

Quick recap:

• A Tree is a collection of nodes connected by edges
• A Binary Tree is a tree, where each node has at most two children, called left and right child
• A Binary Search Tree is a Binary Tree where the values are set so that the left children must be smaller than the parent, the right children - larger