Algorithms | Heap Sort In JavaScript

The topic of today is Heap Sort - a sorting algorithm that is widely used because of its simplicity and efficiency.

It uses heap data structure to find the largest element in each step.

The Definition

Heap sort is a comparison-based algorithm that can be considered as improved Selection Sort.

Like Selection Sort, divides an input into two parts, one sorted and one unsorted.

It reduces the unsorted area iteratively by pulling the largest element from it and inserting it into the sorted area.

It retains the unsorted region in a data structure called heap to find the largest element faster:

The visualization:

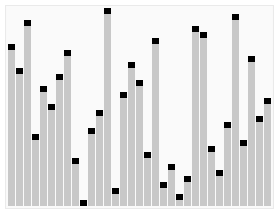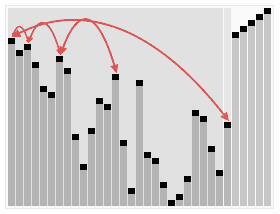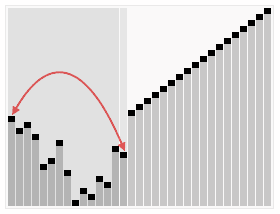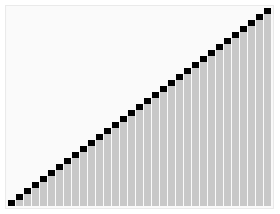
Heap Sort algorithms can be divided into two parts:

• Build a heap out of the data
• Create a sorted array by repeatedly removing the largest element from the heap and inserting it into an array. Once all objects are removed from the heap, we can consider the resulting array can be considered as sorted

What Is Heap?

Heap is a tree-based data structure in which the root node is compared with its children and arranged accordingly.

There are two types of heaps:

• Max heap - the value of the root node is greater than any of its children

• Min heap - the value of the root node is smaller than any of its children

Build A Tree From An Array

Before we build the Heap Sort in JavaScript, it is crucial to understand how array indexes are mapped to tree positions.

Consider the following array:

const arr = [10, 4, 7, 11, 2, 1, 9];

It's binary tree representation:

      10
    /    \
   4      7
  / \    / \
 11  2  1   9

If we observe carefully and assume that the index of any element is i, we can observe the following rules:

• The left child is at index (2*i + 1)
• The right child is at index (2*i + 2)
• The parent is at index (i - 1) / 2

Let's test these rules out:

Index of the "7" is "2"

Then index of the left child is (2 * 2 + 1) = 5
Which equals to "1"

Then index of the right child is (2 * 2 + 2) = 6
Which equals to "9"

Then index of the parent element is (2 - 1) / 2 = 0.5 = ~0
Which equals to "10"

The Complexity

Best-case performance - O(NlogN) if the keys are different and O(N) if the keys are the same.

Worst-case performance - O(NlogN).

Average - O(NlogN).

Pros And Cons

Although it is slower than a well-implemented Quick Sort, it has the advantage of a better worst-case runtime.

Pros

• Efficiency, therefore it is widely used
• Good worst-case scenario
• In-place algorithm

Cons

• Unstable sorting

Implementation In JavaScript

const buildMaxHeap = (arr) => {
  // Get index of the middle element
  let i = Math.floor(arr.length / 2 - 1);

  // Build a max heap out of
  // All array elements passed in
  while (i >= 0) {
    heapify(arr, i, arr.length);
    i -= 1;
  }
}

const heapify = (heap, i, max) => {
  let index;
  let leftChild;
  let rightChild;

  while (i < max) {
    index = i;

    // Get the left child index 
    // Using the known formula
    leftChild = 2 * i + 1;
    
    // Get the right child index 
    // Using the known formula
    rightChild = leftChild + 1;

    // If the left child is not last element 
    // And its value is bigger
    if (leftChild < max && heap[leftChild] > heap[index]) {
      index = leftChild;
    }

    // If the right child is not last element 
    // And its value is bigger
    if (rightChild < max && heap[rightChild] > heap[index]) {
      index = rightChild;
    }

    // If none of the above conditions is true
    // Just return
    if (index === i) {
      return;
    }

    // Else swap elements
    swap(heap, i, index);

    // Continue by using the swapped index
    i = index;
  }
}

const swap = (arr, firstItemIndex, lastItemIndex) => {
  const temp = arr[firstItemIndex];

  // Swap first and last items in the array
  arr[firstItemIndex] = arr[lastItemIndex];
  arr[lastItemIndex] = temp;
}

const heapSort = (arr) => {
  // Build max heap
  buildMaxHeap(arr);

  // Get the index of the last element
  lastElement = arr.length - 1;

  // Continue heap sorting until we have
  // One element left
  while (lastElement > 0) {
    swap(arr, 0, lastElement);
    heapify(arr, 0, lastElement);
    lastElement -= 1;
  }
  
  // Return sorted array
  return arr;
}

Usage In JavaScript

// Assuming that all of functions above are accessible
const arr = [13, 1, 9, 7, 6, 3, 8, 88];

console.log(heapSort(arr)); // Prints "[1, 3, 6, 7, 8, 9, 13, 88]"

Summary

In this article we have covered the basics of the Heap Sort algorithm and found out how it works and why it is one of the most commonly used algorithms.

The implementation may look complicated at first glance, but make sure to try to implement it yourself and the things will look much easier.