Algorithms | Quick Sort In JavaScript

Quick Sort is one of the most popular sorting algorithms developed by the British computer scientist Tony Hoare in 1959 and published in 1961.

If implemented well, it can be about two to three times faster than its main competitors, merge sort and heapsort.

In this article we will learn more about Quick Sort and how it can be implemented most efficiently.

The Definition

Quick Sort is an efficient sorting algorithm that follows the "divide-and-conquer" approach.

It works by selecting a pivot element from the list and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot.

The sub-arrays are then sorted recursively.

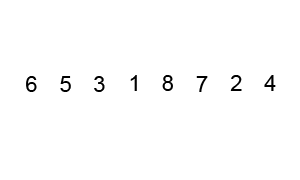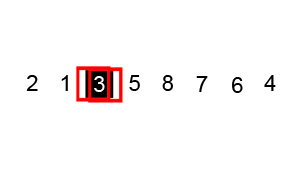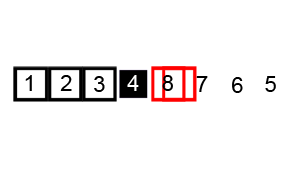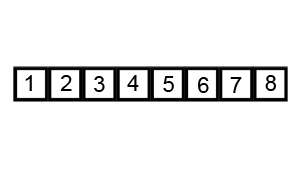
Animated visualization of the quicksort algorithm. The horizontal lines are pivot values:

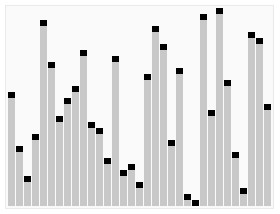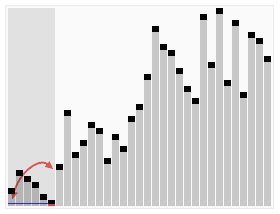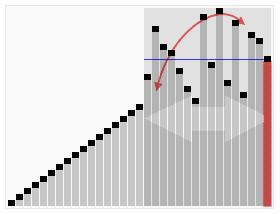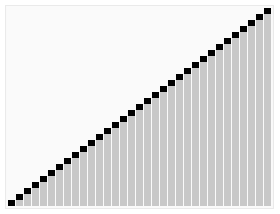
The Complexity

Best-case performance - O(NlogN), if each time we divide an array into two nearly equal or equal pieces.

Worst-case performance - O(N2), if one of the pieces has a length equal to the size N - 1 and it happens repeatedly in every partition.

This can occur if the selected pivot element is the smallest or the largest one on the list, or in some implementations when all elements are equal.

Average - O(NlogN).

Pros And Cons

Even though Quick Sort is an efficient algorithm, the efficiency is majorly impacted by which element is chosen as the pivot point.

Pros

• Simplicity
• High performance if the pivot element was correctly chosen

• Being an in-place algorithm, which means that it requires small additional amounts of memory to perform a sorting operation

  In computer science, an in-place algorithm is an algorithm which transforms input using no auxiliary data structure. However a small amount of extra storage space is allowed for auxiliary variables.

  The input is usually overwritten by the output as the algorithm executes.

  In-place algorithm updates input sequence only through replacement or swapping of elements.

Cons

• The efficiency of the algorithm highly depends on the chosen pivot element. Choosing the wrong one leads to poorer performance

Implementation In JavaScript

const quickSort = (arr, left = 0, right = arr.length - 1) => {
  const length = arr.length;
  
  // Only if there are two or more items, an array is partitioned
  if(length > 1) {
    
    // Partition an array and get the left pointer
    const index = partition(arr, left, right);
    
    // If the left is less than index - 1
    // Then there are still items on the left to be sorted
    if(left < index - 1) {
      quickSort(arr, left, index - 1);
    }
    
    // If the index is less than right
    // Then there are still items on the right to be sorted
    if(index < right) {
      quickSort(arr, index, right);
    }
  }
  
  // If array contains zero or one item, return it
  return arr;
}

const partition = (arr, left, right) => {
  // Get the pivot value from the middle of an array
  const middle = Math.floor((left + right) / 2);
  const pivot = arr[middle];
  
  // Assign the left and right pointers
  let i = left, j = right;
  
  // While there are items in an array to be processed
  while(i <= j) {
    
    // Move left pointer to the right until the value at the
    // left is greater than the pivot value
    while(arr[i] < pivot) {
      i++;
    }
    
    // Move right pointer to the left until
    // The value at the right is less than the pivot value
    while(arr[j] > pivot) {
      j--;
    }
    
    // If the left pointer is less than or equal
    // To the right pointer, then swap values
    if(i <= j) {
      // Perform swap using ES6 syntax
      [arr[i], arr[j]] = [arr[j], arr[i]];
      
      // Shift the pointers so the loop continues in the right spot
      i++;
      j--;
    }
  }
    
  // Return the value of the left pointer because
  // It is used to determine where to start partitioning the next time
  return i;
}

Usage In JavaScript

// Assuming that the quickSort function from the example above is accessible
const arr = [1, 56, 31, 12, 14, 3, 4];

console.log(quickSort(arr)); // Prints "[1, 3, 4, 12, 14, 31, 56]"

Default Sorting In JavaScript

In JavaScript, there is built-in sort function:

const arr = [1, 56, 31, 12, 14, 3, 4];

// Sort in ascending order
console.log(arr.sort((a, b) => a - b)); // Prints "[1, 3, 4, 12, 14, 31, 56]"

// Sort in desceding order
console.log(arr.sort((a, b) => b - a)); // Prints "[56, 31, 14, 12, 4, 3, 1]"

The ECMAscript standard does not specify which sorting algorithm should be used with this function, so different browsers use different algorithms.

For example, Insertion Sort is used by default in Chrome's V8 engine and Merge Sort in Mozilla and Safari.

Summary

Quick sort is an efficient sorting algorithm, based on partitioning the list of elements into smaller arrays that are sorted recursively.

It is extremely fast for larger datasets if the pivot element is selected correctly.